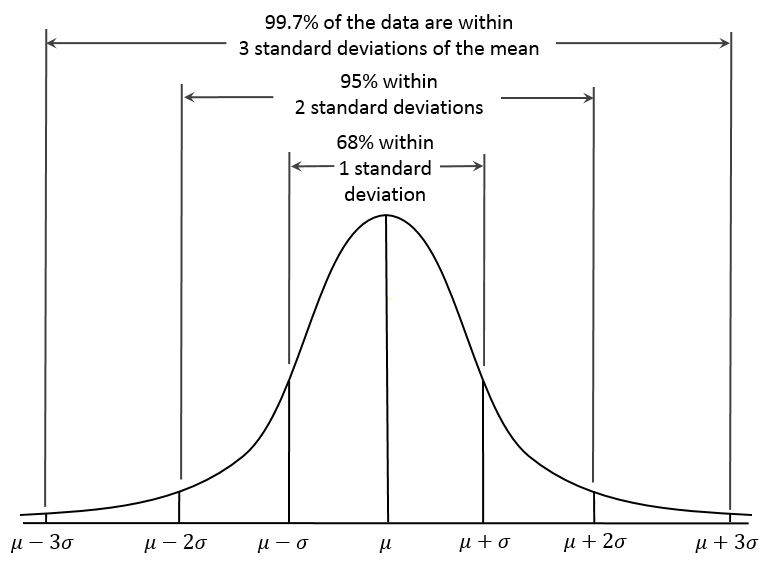
Deviation Value

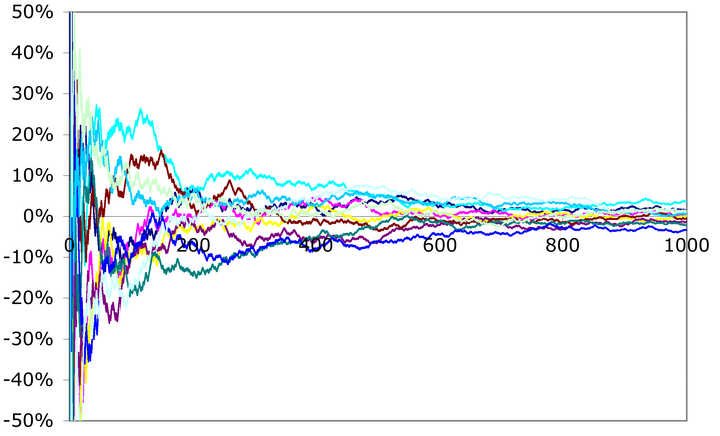
Remember this image?
This is multiple simulated result of a coin tosses stacked together displaying how normal distribution looks like. The results tends to fall within an area, but there are a lot of noise, it is not a very stable, smooth line. In this post, we will learn about the power of deviation.

Back to my favorite example where you have 60% win probability, 1:1 reward ratio, and you risks the optimal size based on Kelly criterion, Repeat this 10 times. Now on average you will win 6, lose 4 right? Based on $1000 capital, you will end up with 1000 x 1.2^6 x .8 ^4 = $1223.059. But what if the result deviates from the average? let's calculate if results was 5/5 or 7/3, the answer is 815.372 and 1834.589.

Let's try to combine the information.
Firstly, deviation is very common. So with a win probability of 60%, it is nothing to be surprise of if you end up with 3/10 or 9/10.
Secondly, 1834.589/1223.059 is 1.5, 1223.059/815.372 is also 1.5.
Deviation value in this situation is 1.5

Deviation value is affected by your risk size and reward ratio, and it heavily impacts your capital. Therefore it is recommended to downplay your expected win probability and reward ratio.

For example in your back test trade result you have 58% win probability and 1.03 average reward per risk, downplay your expectation to 55% and 1, doing that will reduce your risk size, and help you from taking excessive heavy blows to your capital. At the same time it improves your likelihood to outperform your own expectation.