Basics of Compounding

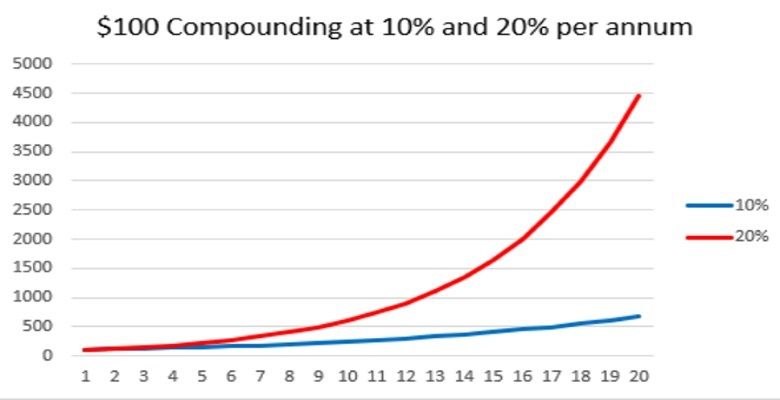
As long as we understand percentage, concept of compounding comes easily.
For example you save $100 in the bank, and the bank gives you 10% interest per year 10% of $100 gives you $10. now you have $110. Next year, the interest is calculated again based on your current figure $110. 10% of $110 is $11, $110 plus $11 is $121. next year $121 plus $12.10 is $133.10 then $146.41 so on.

In your calculator, look for this sign ^

With the above example, input to your calculator 100x110%^4 to represent $100 base money gaining 10% per year compounded for 4 years, you will get the same answer: 146.41

That is compounding for you, you are now able to do any calculations regarding compounding.

Let's say I have $10,000 I saved up in my milo can, the average inflation is 6% per year, I wish to know my buying power in 30 years time. take 10000x94%^3^, and the answer is 1562.55. I would have lost nearly 85% of buying power after 30 years.

If I instead choose to invest them and get an average of 9% return for 30 years, I will have 10000x109%^30 = $132,676.78. even if I estimate to lose 85% of buying power, I would still have roughly $19,900 of today's buying power.

This compounding concept needs to be crystal clear as this will be fundamental for future learning progression.